1. 6 Foot Symbol
2. 6 Foot 6 Inches Symbol

To understand cube roots, first we must understand cubes ...

How to Cube A Number

To cube a number, just use it in a multiplication 3 times ...

Example: What is 3 Cubed?

• It involves the symbol i which stands for the square root of negative one. Or put another way, i 2 = –1. In use, we can use it to express the square root of any negative number. For example This means that the square root of –25 is the square root of +25 times the square root of negative one. For more on imaginary number see Imaginary numbers.
• Square root of some number 'A' is a number 'X' such that 'X' multiplied by itself would be 'A'. Every positive number 'A' has two square roots: positive and negative ±√a. Although the principal square root of a positive number is only one of its two square roots, the designation 'the square root' is often used to refer to the principal square root.

3 Cubed	=
=	3 × 3 × 3	= 27

Note: we write '3 Cubed' as 3³
(the little ³ means the number appears three times in multiplying)

The square root of six √6 = 2.832 How To Calculate Square Roots In mathematics, a square root of a number a is a number y such that y² = a, in other words, a number y whose square (the result of multiplying the number by itself, or y. y) is a. The sixth root of a number is the number that would have to be multiplied by itself 6 times to get the original number. For example, the sixth root of 729 is 3 as 3 x 3 x 3 x 3 x 3 x 3 is 729. The sixth root of 4,096 is 4, as 4 x 4 x 4 x 4 x 4 x 4 is 4,096. For instance, the decimal version of the therefore symbol (∴) would be &‌#8756; The hexadecimal version of the therefore symbol (∴) would be &‌#x2234; Note that the hexadecimal numbers include x as part of the code.

Cubes From 0³ to 6³

0 cubed	=	03	=	0 × 0 × 0	=	0
1 cubed	=	13	=	1 × 1 × 1	=	1
2 cubed	=	23	=	2 × 2 × 2	=	8
3 cubed	=	33	=	3 × 3 × 3	=	27
4 cubed	=	43	=	4 × 4 × 4	=	64
5 cubed	=	53	=	5 × 5 × 5	=	125
6 cubed	=	63	=	6 × 6 × 6	=	216

Cube Root

A cube root goes the other direction:

3 cubed is 27, so the cube root of 27 is 3

3

27

6 Foot Symbol

The cube root of a number is ...
... a special value that when cubed gives the original number.

The cube root of 27 is ...
... 3, because when 3 is cubed you get 27.

Note: When you see 'root' think 'I know the tree, but what is the root that produced it?' In this case the tree is '27', and the cube root is '3'.

Here are some more cubes and cube roots:

64

125

216

Example: What is the Cube root of 125?

Well, we just happen to know that 125 = 5 × 5 × 5 (if you use 5 three times in a multiplication you will get 125) ...

... so the cube root of 125 is 5

6 Foot 6 Inches Symbol

The Cube Root Symbol

This is the special symbol that means 'cube root', it is the 'radical' symbol (used for square roots) with a little three to mean cube root.

You can use it like this: (we say 'the cube root of 27 equals 3')

You Can Also Cube Negative Numbers

Have a look at this:

So the cube root of −125 is −5

Perfect Cubes

The Perfect Cubes are the cubes of the whole numbers:

Perfect Cubes
0	0
1	1
2	8
3	27
4	64
5	125
6	216
7	343
8	512
9	729
10	1000
11	1331
12	1728
13	2197
14	2744
15	3375

It is easy to work out the cube root of a perfect cube, but it is really hard to work out other cube roots.

Example: what is the cube root of 30?

Well, 3 × 3 × 3 = 27 and 4 × 4 × 4 = 64, so we can guess the answer is between 3 and 4.

• Let's try 3.5: 3.5 × 3.5 × 3.5 = 42.875
• Let's try 3.2: 3.2 × 3.2 × 3.2 = 32.768
• Let's try 3.1: 3.1 × 3.1 × 3.1 = 29.791

We are getting closer, but very slowly ... at this point, I get out my calculator and it says:

... but the digits just go on and on, without any pattern. So even the calculator's answer is only an approximation !

(Further reading: these kind of numbers are called surds which are a special type of irrational number)

For example, the third root (also called the cube root) of 64 is 4, because if you multiply three fours together you get 64:

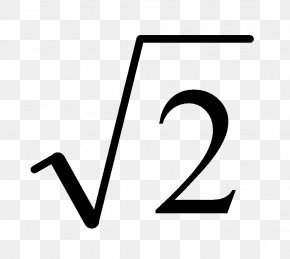This would be written as The above would be spoken as 'the third root of 64 is 4' or 'the cube root of 64 is 4'.

• The second root is usually called the 'square root'.
• The third root of a number is usually called the 'cube root',
• After that, they are called the nth root, for example the 5th root, 7th root etc

Sometimes there are two roots

For every even-degree root (for example the 2nd, 4th, 6th ....) there are two roots. This is because multiplying two positive or two negative numbers both produce a positive result. For example, consider the square root of 9.

What number, multiplied by itself will produce 9?
Obviously 3 will work:

But so will -3:

When there are two roots like this, unless stated otherwise we mean the positive one. So strictly speaking, when we write √4, we mean the positive root, +2. This is called the 'principal root'.

Roots of negative numbers

There are no real even-order roots of negative numbers. For example there is no real square root of -9, because -3 × -3 =+9, and +3 × +3 =+9 also. This applies to all even-order roots, 2nd (square) root, 4th root, 6th root and so on.

However, there are odd-order roots of negative numbers. For example –3 is a cube root of –27. This is because –3 × –3 × –3 = –27. The first two terms when multiplied produce +9, then the next multiply is
+9 × –3 = –27.This applies to all odd-order roots such as 3rd (cube) root, 5th root 7th root etc.

Imaginary numbers

It states above that there is no real square root of a negative number. Note the word 'real'. What this is saying is that there is no real numberthat is the square root of a negative number.

However, in math and engineering we frequently have the need to find the square root of a negative number. To solve this, we introduce the idea of the 'imaginary' number. It involves the symbol i which stands for the square root of negative one. Or put another way, i² = –1

In use , we can use it to express the square root of any negative number. For example This means that the square root of –25 is the square root of +25 times the square root of negative one.

For more on imaginary number seeImaginary numbers.

The symbols

Radicand

The thing you are finding the root of.

Radical symbol

The √ symbol that means 'root of'. The length of the horizontal bar is important. See note below.

Degree

The number of times the radicand is multiplied by itself. 2 means square root, 3 means cube root.After that they are called the 4th root, 5th root and so on.If this is missing, it is assumed to be 2 - the square root.

Another way to write it

Roots can also be written in exponent form. In general So for example the cube root of x would be writtenWhich would be pronounced 'x to the power of one third'.

Other exponents and roots topics